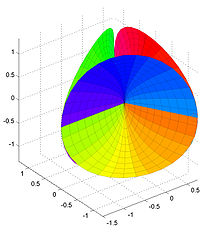
Минимальная поверхность Бура

Минимальная поверхность Бура — это двухмерная минимальная поверхность, вложенная с самопересечениями в трёхмерное евклидово пространство. Поверхность названа именем Эдмонда Бура, работа которого о минимальных поверхностях получила в 1861 году математический приз Французской академии наук.

Описание

Поверхность Бура пересекает себя по трём находящимся в одной плоскости лучам, расходящимися под равными углами из начала координат. Лучи делят поверхность на шесть листов, топологически эквивалентных полуплоскостям. Три листа лежат в верхнем полупространстве и три в нижнем. Четыре листа попарно касаются друг друга на каждом луче.

Уравнение

Точки на поверхности можно параметризовать в полярной системе координат парой чисел ( r , θ ) {displaystyle (r, heta )} . Каждая такая пара соответствует точке в трёхмерном пространстве согласно параметрическому представлению

x ( r , θ ) = r cos ⁡ ( θ ) − ( 1 / 2 ) r 2 cos ⁡ ( 2 θ ) {displaystyle x(r, heta )=rcos( heta )-(1/2)r^{2}cos(2 heta )} y ( r , θ ) = − r sin ⁡ ( θ ) ( r cos ⁡ ( θ ) + 1 ) {displaystyle y(r, heta )=-rsin( heta )(rcos( heta )+1)} z ( r , θ ) = ( 4 / 3 ) r 3 / 2 cos ⁡ ( 3 θ / 2 ) . {displaystyle z(r, heta )=(4/3)r^{3/2}cos(3 heta /2).}

Поверхность можно выразить как решение полиномиальных уравнений порядка 16 в прямоугольной системе координат трёхмерного пространства.

Свойства

Параметризация Вейерштрасса - Эннепера, метод превращения некоторых пар функций от комплексных чисел в минимальные поверхности, порождает эту поверхность для двух функций f ( z ) = 1 , g ( z ) = z {displaystyle f(z)=1,g(z)={sqrt {z}}} . Бур доказал, что поверхности в этом семействе развёртываются в поверхность вращения.